Classifying Images with PyTorch
Posted on Mon 26 February 2024 in Python • 9 min read
Neural networks are something you hear about constantly in the world of machine learning, so in this post we're going to build, train and test a neural network to classify images with PyTorch! We will be using the CIFAR-10 dataset (CIFAR stands for Canadian Institute for Advanced Research), and it's a collection of 60,000 32x32 colour images of 10 different things (which we will refer to as classes). The 10 different classes represent:
- aeroplanes
- cars
- birds
- cats
- deer
- dogs
- frogs
- horses
- ships
- trucks
With each class having 6,000 images each. Specifically for the machine learning side of things, we will be training a convolutional neural network. Convolutional neural networks are particularly good at image problems as they also capture the spatial and temporal dependencies in an image through filtering.
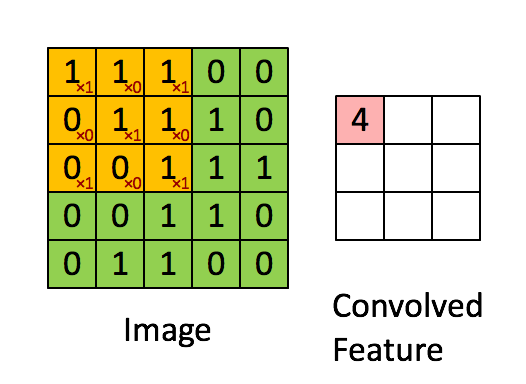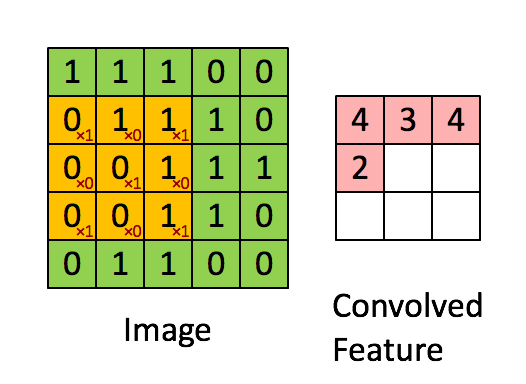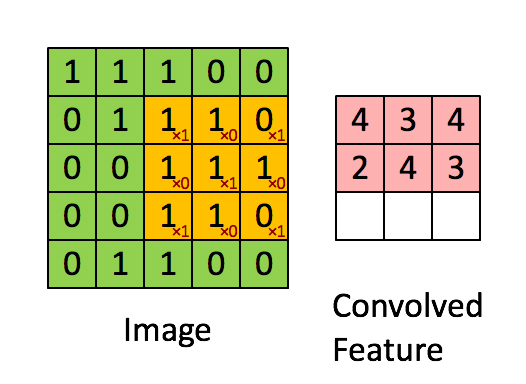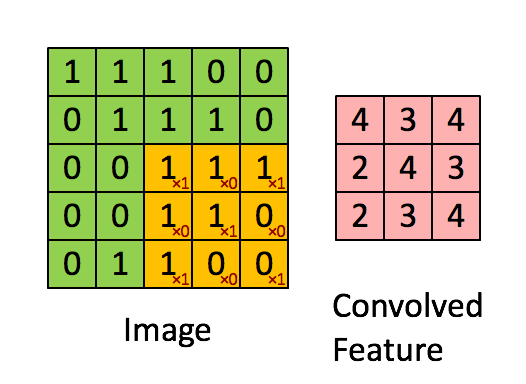
The convolution step in the same refers to the process of filtering the image by a kernal to get an output feature. Best described by the animation below, this is typically followed by pooling steps in an attempt to reduce the dimensionality of the data and make it easier to process.
Let's get into it, as per the recurring theme of these posts, we'll be following the structure:
- Load the data (and split into training/test sets)
- Build the model
- Train the model
- Test the model
For some extra testing in this post, we'll use an example of my actual dog and see what the model thinks she is.
import numpy as np
import torch
import torchvision
import matplotlib.pyplot as plt
from time import time
from torchvision import datasets, transforms
from torch import nn, optim
import torch.nn.functional as F
Get the Data¶
Next we need a method that's going to handle preparing the data in a consistent format, also known as the transformation step. The transformer that we've defined below, first converts the image into a tensor (like a matrix) and then normalizes the values within it. But what does the normalize step mean and particularly why is the value 0.5 chosen for each of the parameters.
Firstly, the normalization step is used is reduce skewness in the data to help the model learn faster, reducing potential noise that could be a distraction to the model. Next there's two tuples which are the parameters to the function, these are sequences for each channel, and given we have colour images, we have 3 channels (red, green and blue) and the first tuple represents the mean for each channel and the second being the standard deviation for each channel.
By transforming our data, this also means when we go to look at the data, we will need to reverse this step to get something understandable to us.
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
Luckily for us, the dataset is available to be used in a compatible way with PyTorch by torchvision. So we download each of the train/test sets and make use of the DataLoader utility in PyTorch to load & apply the transformer to the data for us. We also note that we specify a batch_size here, which means how many inputs will be grouped together when processing, this number is mainly dependant on how much data can be stored in memory on the device.
batch_size = 5
trainset = torchvision.datasets.CIFAR10(root='./data', train=True,
download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size = batch_size,
shuffle=True, num_workers=2)
testset = torchvision.datasets.CIFAR10(root='./data', train=False,
download=True, transform=transform)
testloader = torch.utils.data.DataLoader(testset, batch_size = batch_size,
shuffle=False, num_workers=2)
classes = ('plane', 'car', 'bird', 'cat',
'deer', 'dog', 'frog', 'horse', 'ship', 'truck')
The iter() function in Python creates an iterator for us, which we can then use the next() method, to get the first object in the iterator (ie, the first image in our dataset). Let's use this to inspect the dimesionality of the dataset. As we can see, the images object returns a size of torch.Size([5,3,32,32]) which represents:
- Batch size (5 as defined before)
- Number of channels (3 for colour images)
- Dimensions of image (32x32 pixels)
The labels object is also of size 5 which represents the 5 classes of each image in the batch.
To see this in action, let's visualise the images and their corresponding labels in the first batch.
dataiter = iter(trainloader)
images, labels = dataiter.next()
print(images.shape)
print(labels.shape)
def imshow(img):
img = img / 2 + 0.5 # unnormalize
npimg = img.numpy()
plt.imshow(np.transpose(npimg, (1, 2, 0)))
plt.show()
imshow(torchvision.utils.make_grid(images))
def print_class_labels(match_labels):
class_labels = ""
for i in range(batch_size):
class_labels += f"{classes[match_labels[i]]} "
print(class_labels)
print_class_labels(labels)
Build the Model¶
Now that we've loaded the data, and inspected to see what's inside, it's time to build the model. We do this by extending the nn.Module class from PyTorch with the each of the layers inside our neural network, and define how they are passed 'forward' through the network. Let's break down what's inside each layer and why they were chosen.
Network width is going to represent the number of neurons that will be generated by the convolution steps in the network, this is an interesting hyperparameter as by going too small may cause underfitting or too big could cause overfitting. 16 was chosen arbitrarily as it's half of the dimensions of the input image.
Neural Network Layers¶
Conv1¶
The first layer conv1 represents our first convolution layer, making use of Conv2D to apply convolution as mentioned previously. The number of in_channels will be 3 as we are using colour images (3 for red, green and blue). out_channels represents the number of 'filters' that will be applied to create the same number of neurons in the network. Kernel size represents the size of kernel that will be applied in the convolution step, this number must be odd to represent a square and we will use 3 in particular as to not miss features with a higher number.
Pool¶
The next layer pool is for using MaxPool2d to apply max pooling over the convoluted output from the conv1 and conv2 layers to reduce dimensionality and speed up the training steps later on. We pass in a parameter of 2 which represents the kernel size (and also will represent the stride if not specified), meaning we will be taking the maximum of each 2x2 square of output features from the conv1 output.
Conv2¶
Now we apply convolution again with layer conv2, with the number of input channels now being the number of output channels from the previous convolution. It was noted while researching for this blog post, that it's generally good practice to double the number of output channels for each convolution layer (cannot confirm this though).
FC1¶
FC stands for 'fully connected' layer for which we'll make use of Linear to apply a linear transformation of the output of conv2. This method takes in in_features and out_features, after the 2 convolution layers conv1 and conv2, we have 32 output neurons (double the initial network width) resulting and after pool has been applied twice, our result is reduced to 6*6 (32x32 -> 15x15 -> 6x6). If confused about the size of each output layer, and don't want to calculate it, it can be seen by printing out the shape of x after each step in the forward method. The number of out_features is another hyperparameter, for which a multiple of 8 of the network width was chosen arbitrarily.
Dropout¶
The dropout layer is, as expected, for applying Dropout. Which randomly zeroes some of the elements of the input tensor with a probability of 50% to regularize the input to make our model more robust for inputs. This improves by networks making neurons to work independently of each other.
FC2¶
The last layer of our network is another fully connected layer which we'll use Linear once again to reduce the output of the network back to the number of classes that we intend to predict.
Phew, that was a lot to get through, we define the forward method which will be how values are passed through the layers and instantiate the model so we can begin training!
network_width = 16
class Model(nn.Module):
def __init__(self):
super().__init__()
self.conv1 = nn.Conv2d(in_channels=3,out_channels=network_width,kernel_size=3)
self.pool = nn.MaxPool2d(2)
self.conv2 = nn.Conv2d(in_channels=network_width,out_channels=network_width*2,kernel_size=3)
self.fc1 = nn.Linear(network_width * 2 * 6 * 6, network_width * 8)
self.dropout = nn.Dropout(0.5)
self.fc2 = nn.Linear(network_width * 8, 10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(x.size(0), -1)
x = F.relu(self.fc1(x))
x = self.dropout(x)
x = self.fc2(x)
return x
model = Model()
model
Next we need to decide on the criteria on which our model which will be evaluated upon, which we'll use Cross-Entropy Loss and our optimizer method will be stochastic gradient descent with momentum.
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(), lr=0.003, momentum=0.9)
Train the Model¶
Finally! Now that we've prepared the data, built the model, specified our criteria and optimizer, it's time to train the model. This step follows quite the straightforward approach through iterating through the dataset (in batches):
- We zero the parameter gradients (otherwise PyTorch accumulates the gradients on subsequent backward passes)
- We run our model (forward pass through the network)
- We check how well it went (evaluate loss from the criteria)
- Run a backward pass through the network to calculate the gradient for the optimizer
- Update the model weights
- Repeat steps 1-5 for as many times (epochs) as specified
The longer we train for, the more our model can learn from the data!
time0 = time()
epochs = 10
for e in range(epochs):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
inputs, labels = data
# Zero the parameter gradients (otherwise PyTorch accumulates the gradients on subsequent backward passes)
optimizer.zero_grad()
# Forward Pass through the network
outputs = model(inputs)
# Calculate the loss
loss = criterion(outputs, labels)
# Calculate the gradient
loss.backward()
# Update the weights
optimizer.step()
running_loss += loss.item()
if i == 9999:
print(f"Epoch: {e + 1} loss: {running_loss / 9999}")
running_loss = 0.0
print("\nTraining Time (in minutes) =",(time()-time0)/60)
Now before we do anything else, we want to save the model. This will let us in the future pull up the already trained model to test or even extend without having to repeat the training.
torch.save(model, './my_cifar_model.pt')
Test the Model¶
Now that we've trained the model, it's time to evaluate just how good it performs on the test set of data that we kept separate for this purpose. Let's repeat the same way we took a sneak peak in the training data, to see how our model performed on the first batch in the test data. This may allow us to make some conclusions from our own understanding of similar features between each of the classes.
dataiter = iter(testloader)
images, labels = dataiter.next()
# print images
imshow(torchvision.utils.make_grid(images))
print("Ground Truth:")
print_class_labels(labels)
outputs = model(images)
_, predicted = torch.max(outputs, 1)
print("Predicted:")
print_class_labels(predicted)
What about across the whole dataset? How accurate was our model then?
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
print(f"Accuracy on 10,000 test images {(correct / total) * 100}%")
That's pretty good! Compare it to the 10% chance of random guessing and our model has definitely learnt something! Now we want to be able to calculate each of the classes to see where our model shines and where it doesn't.
class_stats = {}
for output_class in classes:
class_stats[output_class] = {
"correct": 0,
"total": 0
}
with torch.no_grad():
for data in testloader:
images, labels = data
outputs = model(images)
_, predicted = torch.max(outputs, 1)
# Get a tensor of matched labels
c = (predicted == labels)
for i in range(batch_size):
label = labels[i].item()
class_label = classes[label]
if(c[i]):
class_stats[classes[label]]["correct"] += 1
class_stats[classes[label]]["total"] += 1
for output_class in classes:
number_correct = class_stats[output_class]["correct"]
number_total = class_stats[output_class]["total"]
print(f"Accuracy of {output_class}:\t {(number_correct/ number_total) * 100:.2f}%")
Seems like our model works quite well with ships, but not so much dogs... So our next test with my own dog is likely to be wrong, but let's find out! We need to do a few things here:
- Load the image from a file
- Resize it to the 32x32 that was consistent in the CIFAR10 dataset
- Transform it into a tensor with the same transform function
- Evaluate with the model
from IPython.display import Image
pil_img = Image(filename='my-dog.jpg', width=300, height=400)
display(pil_img)
from PIL import Image
def image_loader(path_to_image):
image = Image.open(path_to_image)
resized = image.resize((32,32), Image.ANTIALIAS)
resized.save(path_to_image.split('.')[0] + '-32x32.jpg')
return transform(resized).unsqueeze(0)
my_dog_image = image_loader('my-dog.jpg')
from IPython.display import Image
pil_img = Image(filename='my-dog-32x32.jpg')
display(pil_img)
output = model(my_dog_image)
prediction = int(torch.max(output.data, 1)[1].numpy())
print(f"Prediction: {classes[prediction]}")
 Source:
Source: